GORRO DE BRUJA EN MATEMÁTICAS

Desde el departamento de matemáticas planteamos la siguiente entrada para trabajar en 3º de la ESO pudiendo, simplificando los cálculos, hacerse en 1º y 2º de la ESO. 

Anque el tema es de geometría se trabaja otra serie de competencias que podrían ser interesantes en plástica, tecnología1, economía y lengua. 

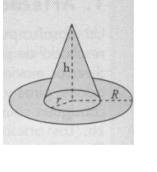
El objetivo es hacer una maqueta de un gorro de bruja, tal y como se muestra en el dibujo. 

Hay una primera parte en la que se plantea la actividad a nivel general. En la segunda parte se hace referencia a los objetivos de la misma y las posibles adaptaciones que pueden hacer las otras materias. 

PARTE I 

Ejercicio: Para carnaval nos queremos disfrazar de brujo/as. Hemos pensado en confeccionar unos gorros con cartulina como el del dibujo. 

a) Calcula la cantidad de cartulina necesaria para hacer un sombrero siendo R=20cm, r=9 cm y h= 30cm. 

b) Sabiendo que las cartulinas que tenemos son de 50cmx65cm, ¿cuántas cartulinas necesitaré para hacer cada gorro? 

Instrucciones: 

1. Al no disponer de cartulinas deberemos adaptar las medidas del folio para que sea proporcional a la cartulina. Es posible que debamos transformar el tamaño del folio para construir nuestro gorro a escala. 

2. Una vez tenemos el folio a escala, deberemos emplear la razón de proporcionalidad para adaptar todas las medidas del ejercicio. 

3. Descomponemos el gorro en dos figuras. Y las dibujamos con las medidas calculadas. Para ello necesitaremos calcular la generatriz y el ángulo que forma la parte del cono. 

4. Recortamos cada una de las piezas (2 partes, corona circular y parte lateral del cono). ¿cuántas cartulinas necesitaríamos para hacer un gorro? ¿por qué? 

5. Presentación y reflexión: Al finalizar la actividad, presentaremos las creaciones a los compañeros explicando las dificultades que nos hemos encontrado en su elaboración 

PARTE II 

Objetivos de la actividad:	Actividades concretas para las diferentes materias planteadas
1. Aplicar conceptos geométricos: Los estudiantes deberían ser capaces de aplicar los conceptos de geometría, para construir el gorro de bruja con las dimensiones adecuadas.	En lengua se podría trabajar la elaboración de un glosario de todos los términos matemáticos, económicos …, que nos fuesen apareciendo.
2. Comprender la relación entre las formas tridimensionales y bidimensionales: Los alumnos deben comprender cómo las formas tridimensionales, como el cono, se relacionan con las formas bidimensionales, como los círculos, y cómo estas formas se utilizan en la construcción del gorro de bruja.	En economía se podría plantear elaborar un presupuesto previo de los materiales necesarios. La eficiencia en el uso de los mismos. Trabajar la escasez de los recursos naturales y enlazarlo con los ODS de la agenda 20302
3. Aplicar conceptos de escalas y razón de proporcionalidad para ajustar las dimensiones iniciales del gorro de bruja al tamaño de un folio estándar, los alumnos deben ser capaces de comprender y aplicar los conceptos de escalas y calcular la razón de proporcionalidad para ajustar todas las medidas del gorro de bruja, incluyendo la altura, el radio de la base del cono y el radio de la corona circular, de manera proporcional al tamaño de un folio estándar.	En matemáticas de 1ºy 2º se les puede facilitar estos cálculos.
4. Fomentar habilidades de resolución de problemas: Los estudiantes deberían desarrollar habilidades para resolver problemas al enfrentarse a desafíos durante su construcción.
5. Promover el trabajo en equipo y la colaboración: Los alumnos deben trabajar juntos en grupos para construir los gorros de bruja, lo que fomenta el trabajo en equipo, la colaboración y la comunicación efectiva entre ellos.
6. Fomentar la creatividad al permitir que los estudiantes decoren sus gorros de bruja de acuerdo con su imaginación y estilo personal. Pueden usar colores, brillos, etc., para hacer sus gorros únicos y originales.	En plástica se puede plantear el uso de materiales reciclados. Se puede trabajar la sostenibilidad .
7. Reflexionar sobre el proceso de aprendizaje: Al finalizar la actividad, los estudiantes deben ser capaces de reflexionar sobre lo que han aprendido durante el proceso, cómo han aplicado los conceptos de geometría llevados a la práctica y cómo pueden mejorar en el futuro.

1 No se especifica actividad concreta para la materia de tecnología. Se considera al igual que en matemáticas que todos los apartados son de interés.

2 Hacer referencia a los ODS se puede hacer desde cualquiera de las materias